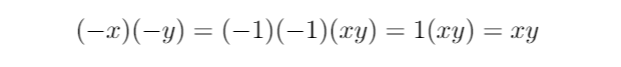วันก่อนโดนถามว่า “ทำไมจำนวนลบคูณจำนวนลบแล้วได้จำนวนบวกเฉยเลยอะ” นี่ถึงกับต้องปาดเหงื่อไม่รู้จะอธิบายยังไงให้ง่ายต่อการเข้าใจเลย คือคำถามที่ดูเหมือนเป็นพื้นฐานหรือดูไม่มีพิษสงมากเท่าไหร่ การให้เหตุผลก็ทำได้ยากมากเท่านั้น เพราะจะถูกจำกัดเครื่องมือให้ใช้ได้ไม่กี่อย่าง โดยเครื่องมือที่ใช้ได้เหล่านั้นจะต้องไม่ได้เกี่ยวข้องกับสิ่งที่กำลังให้เหตุผลอยู่หรือผลของมันด้วย (ทำไม?)

ลองนึกภาพตามว่าหากไปใช้ผลลัพธ์ของสิ่งที่กำลังให้เหตุผลอยู่หรือที่แย่ไปกว่านั้นคือการนำสิ่งที่กำลังให้เหตุผลมาเป็นเหตุผลเองเลย มันจะดูมึนๆ งงๆ จนต้องเผลอร้องออกมาว่าอิหยังวะแน่นอน ยกตัวอย่างเช่น

• A: ลุงคนนี้เป็นคนดีที่ดีกว่าคนอื่นเป็นไหนๆ
• B: รู้ได้ไงอะ
• A: ก็ไม่เห็นคนอื่นดีเท่าลุงเลยอะ

สิ่งที่ A ทำคือการนำข้อความที่ควรจะต้องแสดงเหตุผลมาใช้สนับสนุนสิ่งที่กำลังให้เหตุผลหรือพิสูจน์อยู่ ซึ่งปรากฏการณ์นี้เรียกว่า circular reasoning มันคือความพังอย่างหนึ่งในการให้เหตุผล เพราะเหตุผลที่ยกมามันคือสิ่งที่ต้องพิสูจน์ เราไม่สามารถไปเอาตัวมันเองมาใช้เป็นเหตุผลเพื่อสรุปว่าสิ่งที่กล่าวอ้างเป็นความจริงได้ ต้องหาเหตุผลอื่นมาโน้มน้าวแทน

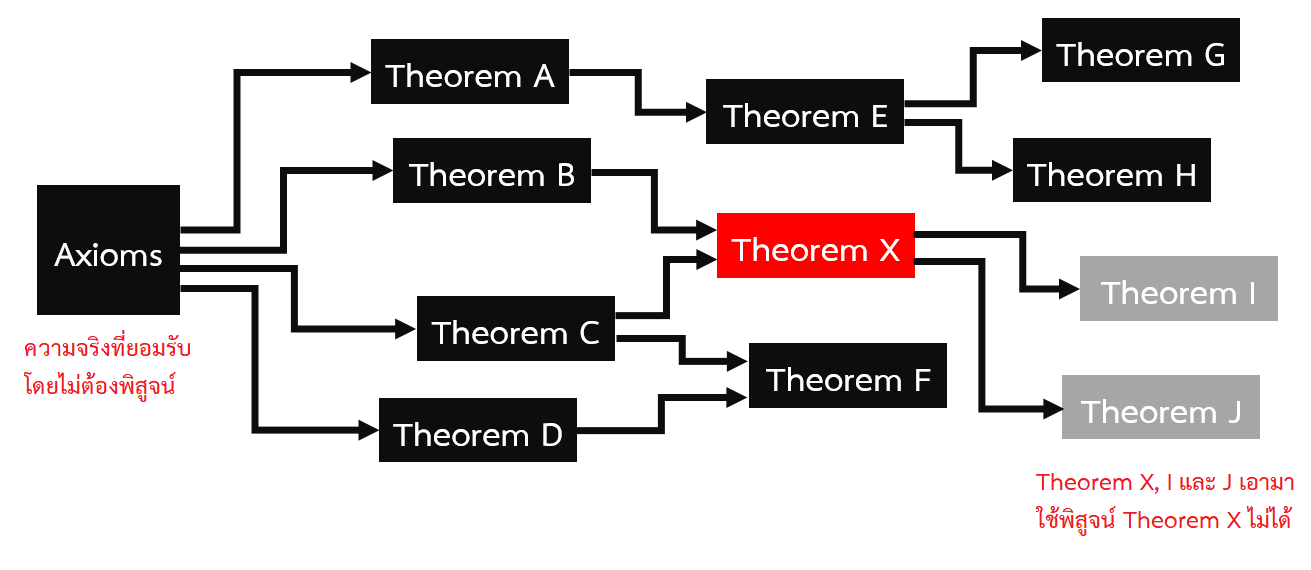
สมมติว่าต้องการพิสูจน์ทฤษฎี X สิ่งที่เราสามารถใช้มาเป็นเหตุผลในการสรุปว่าทฤษฎี X เป็นจริงได้ก็คือก้อนสี่เหลี่ยมทุกอันเลยยกเว้นตัวมันเอง (ทฤษฎี X) และผลของมัน (ทฤษฎี I และ J) ด้วยเหตุนี้มันเลยกลายเป็นว่ายิ่งย้อนกลับไปถามคำถามที่ลึกมากเท่าไหร่ สิ่งที่ใช้ในการอธิบายความเป็นไปของมันก็อาจจะมีน้อยและอาจเป็นแนวคิดที่ลึกแบบจับต้องได้ยากมากขึ้นเท่านั้น

กลับมาที่การพิสูจน์ว่าจำนวนลบคูณกับจำนวนลบแล้วได้ค่าบวก ความยากอย่างหนึ่งคือการมองไม่เห็นภาพเพราะไม่สามารถถอดความว่าเป็นการบวกซ้ำกันหลายๆ ครั้งได้ ซึ่งเอาจริงการตีความหมายแบบนี้มันใช้ได้แค่กับจำนวนนับ (จำนวนเต็มบวก) เท่านั้น แล้วจากนั้นถึงขยายแนวคิดการคูณไปยังจำนวนชนิดอื่นๆ ทำให้เราไม่สามารถแปลสัญลักษณ์ -3.14

×-2.72 ว่าเป็นการบวก -3.14 ไป -2.72 ครั้ง เพราะ -2.72 ครั้งมันไม่มีความหมายในโลกมนุษย์

ดังนั้นวิธีในการแสดงเหตุผลก็ต้องเป็นทางพีชคณิตเท่านั้น แต่นั่นก็จะมีความยากลำบากของการหาเหตุผลมาสนับสนุนอีก ด้วยความที่เรามาอยู่ในยุคที่มีเครื่องมือทางคณิตศาสตร์อยู่เต็มไปหมด แล้วเราอาจหาเหตุผลมาอ้างแล้วดันเกิดลูปของการให้เหตุผลแบบพังๆ โดยไม่รู้ตัวก็ได้ เช่น

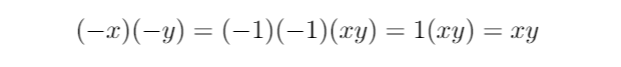
1. สมมติให้ x และ y เป็นจำนวนจริงที่มีค่าเป็นบวก ดังนั้น -x และ -y จะเป็นจำนวนจริงที่มีค่าเป็นลบ จากนั้นใช้คุณสมบัติว่า (-a) = (-1)a สำหรับทุกจำนวนจริง a ทำให้ได้ว่า -x = (-1)x และ -y = (-1)y
2. ใช้คุณสมบัติการสลับที่และการเปลี่ยนกลุ่มของการคูณของจำนวนจริงในการจัดรูปใหม่
3. แทนค่า (-1)(-1) = 1
4. เนื่องจาก 1 เป็นเอกลักษณ์การคูณ นั่นหมายถึงว่า เอา 1 ไปคูณกับอะไรก็ได้ตัวนั้น

อันนี้ต้องบอกด้วยความเขินอายว่าเป็นวิธีที่ใช้ตอบคำถามในตอนนั้น ซึ่งเมื่อย้อนมาคิดอีกที อ้าว ตรรกะเราพังนี่หว่า ให้ทายกันว่าผิดที่ข้อไหน 1, 2, 3 หรือ 4

ใช่แล้วครับ ข้อที่ทำให้ทุกสิ่งทุกอย่างพังทลายและดูไม่น่าเชื่อถืออีกต่อไปก็คือข้อ 3 เพราะสิ่งที่กำลังให้เหตุผลหรือพิสูจน์อยู่นั้นคือ “จำนวนลบคูณกับจำนวนลบแล้วมีค่าเป็นบวก” แต่เราดันใช้ผลลัพธ์ของสิ่งที่กำลังพิสูจน์อยู่นี้ไปกับการบอกว่าค่าของ (-1)(-1) มีค่าเท่ากับ 1 หากเราสามารถสร้างความชอบธรรมให้กับขั้นตอนที่ 3 ได้โดยการตอบให้ได้ว่าทำไมมันเท่ากับ 1 โดยหาเหตุผลอื่นที่ไม่ได้เกี่ยวข้องกับสิ่งที่ต้องพิสูจน์ แล้วบทพิสูจน์นี้ก็จะถือว่าโอเคอยู่

ดังนั้นเราต้องมาพิสูจน์ว่า (-1)(-1) = 1 โดยไม่ให้เกิด circular reasoning ซึ่งก็สามารถทำได้โดยการใช้ประโยชน์จากเอกลักษณ์การบวกและเอกลักษณ์การคูณ ดังนี้

ทีนี้เมื่อเราสามารถแสดงให้เห็นได้แล้วว่า (-1)(-1) = 1 จริงๆ โดยไม่ได้แอบไปใช้สิ่งที่กำลังพิสูจน์หรือผลของมันเลย ใช้แต่เหตุผลอื่นล้วนๆ ทำให้ขั้นตอนที่ 3 ในการพิสูจน์ก่อนหน้าสมเหตุสมผลแล้ว และมันก็ทำให้บทพิสูจน์โดยรวมทั้งหมดสมเหตุสมผลตามมา (บทพิสูจน์ตัวเต็มอยู่ด้านล่าง)

เท่าที่ไปเสิร์ชมาก็พบว่ามีหลายวิธีในการให้เหตุผลชวนให้เชื่อว่าลบคูณลบได้บวก ตั้งแต่การจินตนาการว่ากำลังเดินอยู่บนเส้นจำนวน การยืมเงิน การดูแพทเทิร์น หรือแม้กระทั่งการสมมติว่าถ้าลบคูณลบไม่ได้เป็นบวกแล้วมันจะเกิดข้อขัดแย้ง แต่ทุกอย่างที่กล่าวมานี้ก็ขอให้ดูผ่านๆ แบบพอหอมปากหอมคอ เพราะมันซุกซ่อนการให้เหตุผลแบบพังๆ อยู่ หรือบางอันก็บอกไม่ครบทุกกรณีจนมันไม่สามารถใช้เป็นข้อสรุปอะไรได้เลย (แต่ก็เนียนๆ สรุปไปเลยแล้วกัน!)

จริงๆ แล้วความพังของการใช้เหตุผลนี่เกิดขึ้นบ่อยและมาได้หลายรูปแบบมาก ก็ขอให้อยู่รอดปลอดภัย มีเหตุผลที่สมเหตุสมผลแล้วกัน อย่าให้สิ่งที่ลุ่มหลงหรือคลั่งไคล้มาทำให้ตรรกะบิดเบี้ยวไปได้!

 

บทพิสูจน์แบบละเอียด (กว่าเดิม)

สมมติว่า 0(x) = 0 สำหรับจำนวนจริง x อะไรก็ได้ และการบวก การคูณพื้นฐานของจำนวนจริงเป็นความรู้พื้นฐาน

1. พิสูจน์สิ่งที่ต้องใช้ว่า -x = (-1)x สำหรับทุกจำนวนจริง x

ด้านซ้ายของเครื่องหมายเท่ากับคือสัญลักษณ์แทน “อินเวอร์สการบวกของ x” ส่วนด้านขวาเป็นการบอกว่ามันคือการคูณ x ด้วย -1 ดังนั้นแปลสัญลักษณ์ทางคณิตศาสตร์เป็นภาษาคนได้ว่า อินเวอร์สการบวกของ x ก็คือการเอา -1 มาคูณกับ x

2. สมมติให้ x และ y เป็นจำนวนจริงบวก เพราะฉะนั้นอินเวอร์สการบวกของมันก็คือ -x และ -y ตามลำดับ แล้วพิจารณาที่ผลคูณของอินเวอร์สทั้งสอง จากนั้นใช้การเปลี่ยนกลุ่มและการสลับที่ของการคูณมาจัดรูปให้สวยงาม

3. พิสูจน์ว่า (-1)(-1) = 1

4. เขียนใหม่อีกครั้งเพื่อสรุปขั้นตอนทั้งหมด

References

1. circular reasoning fallacy
2. why is negative times negative positive?
3. stack exchange
4. walking along the number line
5. six ways to show that the product of two negative real numbers is positive
6. the contradiction will occur if otherwise